Fraccions equivalents: mètodes per resoldre-les i exemples

Què són les fraccions equivalents?

Les fraccions equivalents són aquelles que tenen diferents numeradors i denominadors però tenen el mateix valor.

Per exemple:

2/4 i 3/6

Són fraccions equivalents, perquè ambdues són iguals a ½.

Una fracció és part d’un tot. Les fraccions equivalents representen la mateixa porció del tot.

Per a cada fracció, podem trobar la seva fracció equivalent multiplicant tant el numerador com el denominador pel mateix número.

Per exemple:

Hem de trobar la tercera fracció equivalent de ⅔; llavors hem de multiplicar 2/3 per 3/3.

Per tant, 2/3 × (3/3) = 6/9, és la fracció equivalent a 2/3.

Les fraccions són equivalents si ambdues resulten la mateixa fracció després de la simplificació.

Diguem que a/b i c/d són dues fraccions, després de la simplificació d’aquestes fraccions, ambdues resulten en fraccions equivalents, diguem e/f, llavors són iguals entre sí.

Per exemple, la fracció equivalent de 1/3 és 5/15, perquè si simplifiquem 5/15, llavors la fracció resultant és la mateixa.

La pregunta més important aquí pot ser: per què tenen valors iguals malgrat tenir números diferents?

La resposta a aquesta pregunta és que, com el numerador i el denominador no són nombres coprimers, tenen un múltiple comú, que en dividir-lo dona exactament el mateix valor.

Exemple de fracció equivalent

1/2 = 2/4 = 4/8

Es veu clarament que les fraccions anteriors tenen diferents numeradors i denominadors.

Dividint tant el numerador com el denominador pel seu factor comú, tenim:

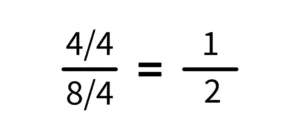
De la mateixa manera, si simplifiquem 2/4, novament obtenim 1/2.

Fraccions equivalents d’una fracció mixta:

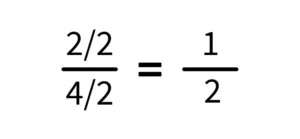
Considerem una fracció mixta per a trobar la seva fracció equivalent.

Fracció mixta = 1 ½

Ara, convertim aquesta fracció en una fracció impròpia.

1 ½ = (1 × 2 + 1)/2 = (2 + 1)/2 = 3/2

Les fraccions equivalents de la fracció anterior són:

3/2 = (3 × 2)/(2 × 2) = 6/4
3/2 = (3 × 3)/(2 × 3) = 9/6
3/2 = (3 × 4)/(2 × 4) = 12/8

i així successivament.

Com trobar fraccions equivalents?

Les fraccions equivalents s’avaluen multiplicant o dividint tant el numerador com el denominador pel mateix número.

Per tant, les fraccions equivalents, reduïdes al seu valor simplificat, seran totes iguals.

Multiplicar numerador i denominador pel mateix número

Per exemple, considerem la fracció 1/5

• Multiplicant numerador i denominador per 2, obtenim 1/5 × 2/2 = 2/10
• Multiplicant numerador i denominador per 3, obtenim 1/5 × 3/3 = 3/15
• Multiplicant numerador i denominador per 4, obtenim 1/5 × 4/4 = 4/20

Per tant, podem concloure que,
1/5 = 2/10 = 3/15 = 4/20

Dividir numerador i denominador pel mateix número

Per exemple, necessitem trobar la fracció equivalent de 18/32.

Troba el màxim comú divisor de 18 i 32.

MCD (18, 32) = 2

Ara divideix el numerador i el denominador entre 2, per a obtenir la fracció equivalent a 18/32.

(18 ÷2)/(32÷2) = 9/16

Per tant, 9/16 equival a 18/32.

Nota: Només podem multiplicar o dividir pels mateixos números per a obtenir una fracció equivalent i no sumes ni restes. La simplificació per a obtenir números equivalents es pot realitzar fins al punt en què tant el numerador com el denominador continuïn sent nombres enters.

Mètodes per a determinar fraccions equivalents

Com podem determinar si dues fraccions són equivalents o no? És possible mitjançant aquests mètodes:

• Mètode 1: fer que els denominadors siguin iguals.
• Mètode 2: multiplicació creuada.
• Mètode 3: convertir a decimals.

Mètode 1:

En igualar els denominadors, podem avaluar si dues fraccions són equivalents.

Per exemple, troba si 2/3 i 6/9 són equivalents.

MCM de 3 i 9 = 9

Multiplica 2/3 per 3/3 perquè el denominador sigui igual a 9.

2/3 × 3/3 = 6/9

Per tant, en igualar els denominadors, podem veure que 2/3 i 6/9 són fraccions equivalents.

Mètode 2:

Dues fraccions 1/2 i 3/6

Multiplica totes dues fraccions per a obtenir:

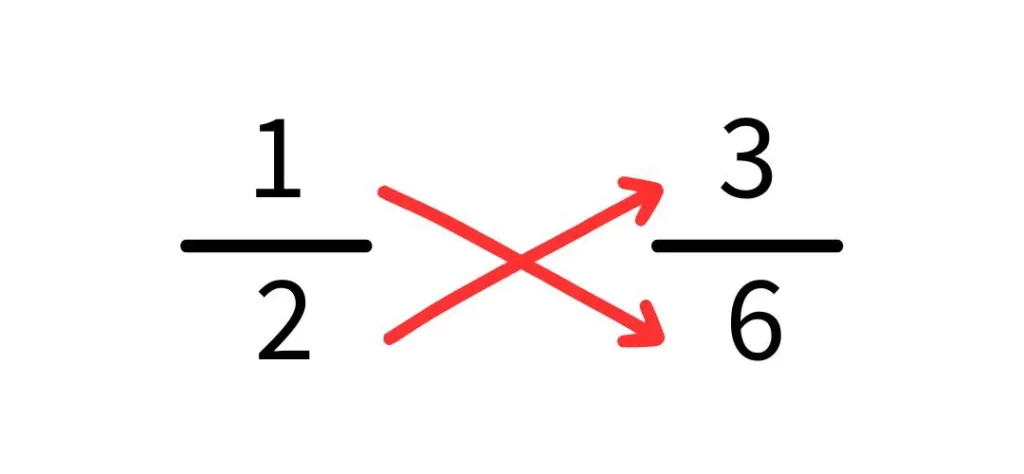
1 x 6 = 6
2 x 3 = 6

Atès que tots dos valors són iguals, 1/2 i 3/6 són fraccions equivalents.

Mètode 3:

Si es donen dues fraccions, simplement podem trobar els seus decimals per a comprovar si són fraccions equivalents.

Comprovem si 1/4 i 3/12 són fraccions equivalents convertint-les a forma decimal.

1/4 = 0,25
3/12 = 0,25

Atès que totes dues fraccions donen com a resultat el mateix decimal, són equivalents.

Exemples resolts

Exemple 1:

Les fraccions donades 5/16 i x/12 són fraccions equivalents, després troba el valor de x.

Solució:

5/16 = x/12

x = (5 × 12)/16
x = 60/16
x=15/4

Per tant, el valor de x és 15/4.

Exemple 2:

Dues fraccions 3/5 i 4/x són equivalents. Troba el valor de x.

Solució:

3/5 = 4/x
x = (4 × 5)/3
x = 20/3

Exemple 3:

Quines fraccions són iguals a ¼?

Solució: Per a trobar fraccions equivalents de ¼ necessitem multiplicar el numerador i el denominador pels mateixos números. Per això,

¼ × (2/2) = 2/8
¼ × (3/3) = 3/12
¼ × (4/4) = 4/16
¼ × (5/5) = 5/20

Etcètera.

Preguntes de pràctica

1. Troba la fracció equivalent de 8/10
2. Quina és la forma més simple del 81/9?
3. Escriu la fracció tres setens com una fracció equivalent amb un denominador de 21.
4. Escriu la fracció cinc vuitens com una fracció equivalent amb un denominador de 24.

Normalment, les fraccions equivalents es comencen a aprendre a 6è de primària. Nosaltres les expliquem al nostre quadern Pont de 6è de primària.