Com resoldre multiplicacions de tres xifres

En aquest post d’Editorial Nadal t’expliquem les multiplicacions de tres xifres. Quan aprens a multiplicar per tres xifres, multiplicar per més dígits es fa més fàcil, ja que sempre se segueix el mateix mecanisme. Esperem que després de llegir aquest article entenguis com es fa i et sigui molt més fàcil.

Quan multipliquem números de tres xifres, ordenem els números en columnes d’acord amb els valors posicionals. Sabem que els números de tres xifres estan ordenats segons el seu valor posicional com a unitats, desenes i centenes.

Una vegada tenim un conjunt de dos números per a multiplicar, generalment mantenim el número major a dalt i el menor sota. El número que es col·loca damunt es converteix en el multiplicant i el número escrit sota és el multiplicador.

Quan els números s’ordenen segons el seu valor posicional, multipliquem el multiplicador amb tots els dígits del multiplicant d’un en un començant des del dígit de les unitats, seguit pel dígit de les desenes i després el dígit de les centenes. Tots aquests productes s’escriuen junts i donen com a resultat el producte final

Per exemple, si necessitem multiplicar 123 × 3, els col·loquem com veieu a continuació:

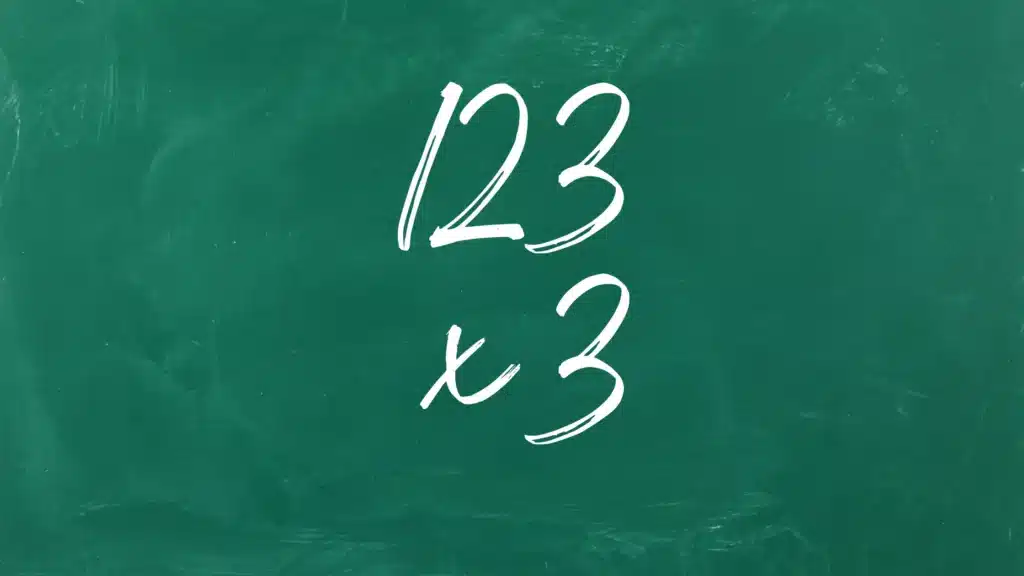
On 123 és el multiplicant i 3 és el multiplicador. Després de multiplicar aquests números obtenim el producte 269.

Passos per a les multiplicacions de tres xifres

Exemple:
Multiplicar 123 per 456.

Pas 1:

Organitza els números 123 i 456 en columnes segons els seus valors posicionals.

Pas 2:

Multiplica 6 per cada xifra de 123.

Quan multipliquem 6 per 3, obtenim 18. Com 18 és un número de 2 dígits, escrivim 8 sota la columna de les unitats i portem 1 a la columna de les desenes, damunt del 2.

Quan multipliquem 6 per 2, obtenim 12. Ara, sumem l’1 arrossegat a 12 i obtenim 13. Com 13 és un número de 2 dígits, escrivim 3 sota la columna de les desenes i portem 1 a la següent columna, damunt del 1.

Quan multipliquem 6 per 1, obtenim 6. Ara, sumem l’1 arrossegat a 6 per a obtenir 7. Com no queda cap altre dígit per a la multiplicació, escrivim 7.

Llavors, tenim 738 en la primera línia com a producte parcial.

Pas 3:

Ara, col·loca un zero sota aquest producte parcial en la columna de les unitats. Això es deu al fet que en aquest pas en realitat estem multiplicant 123 per 50.

Pas 4:

Multiplica 5 per cada xifra de 123.

Quan es multiplica 5 per 3, obtenim 15. Com 15 és un número de 2 xifres, escrivim 5 en la columna de les desenes i portem 1 a la següent columna damunt de 2.

Quan multipliquem 5 per 2, obtenim 10. Ara, sumem l’1 arrossegat a 10 per a obtenir 11. Com 11 és un número de 2 dígits, escrivim 1 en la columna de centenes i portem 1 a la següent columna damunt de 1.

Quan multipliquem 5 per 1, obtenim 5. Ara, sumem l’1 arrossegat a 5 per a obtenir 6. Com no queda cap altre dígit per a la multiplicació, escrivim 6. Llavors, tenim 6150 en la segona línia del producte parcial.

Pas 5:

Ara, col·loca dos zeros (0) sota la columna de les unitats i les desenes sota el producte parcial obtingut en el pas anterior. Això es deu al fet que en aquest pas en realitat estem multiplicant 123 per 400.

Pas 6:

Multipliquem 4 per cada dígit de 123.

Quan multipliquem 4 per 3, obtenim 12. Com 12 és un número de 2 dígits, escrivim 2 sota la columna de les centenes i portem 1 a la següent columna damunt de 2.

Quan multipliquem 4 per 2, obtenim 8. Ara, sumem l’1 arrossegat a 8 per a obtenir 9. Escrivim 9 en la següent columna.

Quan multipliquem 4 per 1, obtenim 4. Com no queda cap altre dígit per a la multiplicació, escrivim 4. Llavors, tenim 49.200 en la tercera línia com a producte parcial.

Pas 7:

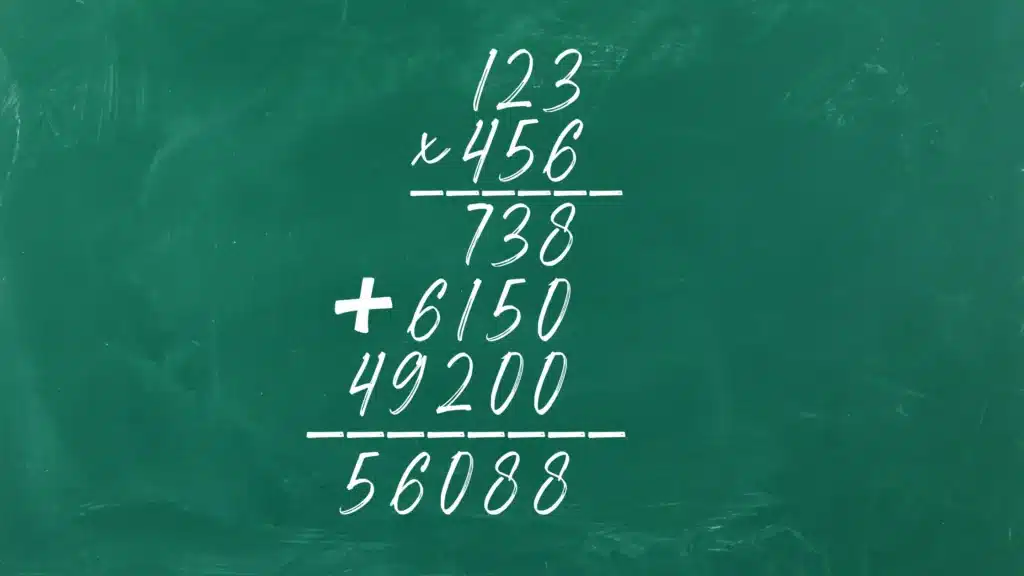
Agrega els 3 productes parcials per a obtenir el producte final. Això significa 738 + 6.150 + 49.200 = 56.088.
Per tant, el producte final és 56.088.